Posted: 15 Jul 2014 04:15 AM PDT
Por: Rafael Gama Vieira
 |
Figura 1: Helicóptero.
|
Você sabe dizer qual a relação entre o movimento de um atleta de patinação no gelo e o funcionamento de um helicóptero?
Certamente você já percebeu que um patinador realiza diversos giros durante uma apresentação e que sua velocidade é alterada num mesmo movimento, sendo possível, então, girar mais rápido e mais devagar, conforme o atleta queira.
Mas como ele faz para mudar esta velocidade e conseguir girar tão rápido?
Em relação aos helicópteros, como é possível obter uma precisão no vôo e por que eles possuem duas hélices, sendo uma pequena em sua cauda?
A explicação para estes dois fenômenos é a chamada Conservação de Momento Angular, estudada na disciplina de Física.
 |
Figura 2: Carro em movimento.
|
Para entender o que é momento angular, começaremos pelo caso mais simples, o momento linear ou quantidade de movimento linear.
Na imagem ao lado temos um carro em movimento. Sabemos então que, neste caso, ele possui uma massa m e uma velocidade v. O momento linear, denominado por P, será então o produto destas duas grandezas.
Logo:
Analisando a equação podemos dizer que, todo corpo que possui massa e está em movimento, ou seja, tem uma velocidade, tem então um momento linear associado.
Considere agora uma partícula de massa m em um movimento circular, como mostra a figura 3.
 |
Figura 3: Partícula em movimento circular. www.estudiarfisica.wordpress. |
Chamamos de r o raio desta trajetória. Temos agora o que chamamos de momento angular, ou quantidade de movimento angular, representado por um vetor perpendicular ao plano de movimento, denominado por L e dado pela equação a seguir:
onde w é a velocidade angular do móvel.
O produto mr² é conhecido como momento de inércia de um corpo e varia de acordo com sua forma.
Em resumo, podemos dizer que quando um móvel executa um movimento de translação, este possui um momento LINEAR e quando executa um movimento de rotação, possui um momento ANGULAR.
Como todas as outras grandezas físicas, o momento angular tende a ser conservado, ou seja, ao alterarmos um dos valores da equação 2, o resultado final deve continuar o mesmo.
Vamos analisar o caso da patinadora: consideramos o raio r da atleta como sendo a distância entre o seu eixo de rotação e sua mão, como mostra a figura 4.
 |
Figura 4: Patinadora com os braços abertos.
|
Ao considerarmos a patinadora realizando um movimento de rotação, podemos dizer que ela possui massa, um raio e uma velocidade angular, logo, possui um momento angular.
Considere agora que a patinadora fecha e abre os braços durante a rotação, variando então seu valor de r. Como mencionado anteriormente, o valor do momento angular deve ser conservado, ou seja, ao fechar os braços (Figura 5), o raio da atleta diminui, logo, para manter o mesmo valor de L, sua velocidade angular w deve aumentar. Para facilitar o entendimento, usaremos um exemplo numérico.
 |
Figura 5: Patinadora com os braços fechados.
|
Considere a massa da patinadora como 60Kg, seu raio com os braços abertos igual a 1,0 m e sua velocidade angular neste caso como 10 rad/s. Substituindo estes valores na equação 2 temos:
Agora, consideramos que, ao fechar os braços, seu raio diminua para 0,3 m. Sabemos que o valor de L deve ser 600kg.m² rad/s. Basta então substituir estes valores na equação 2 e encontrar o valor da nova velocidade angular.
Evidenciando w na equação 2 temos:
Podemos ver que a velocidade angular da patinadora aumenta 4 vezes quando ela fecha os braços. Logo, para girar mais rápido basta fechar o máximo possível os braços e as pernas e abri-los para girar mais devagar.
No caso do helicóptero temos novamente o momento angular quando suas hélices começam a girar e este, como sempre, tende a se conservar.
Considere o helicóptero inicialmente parado e com as hélices desligadas. Neste caso o momento angular L é igual a zero e este é o estado inicial do sistema. Quando esta hélice é ligada, instantaneamente temos o surgimento do momento angular. Porém o momento L do sistema deve ser conservado, ou seja, manter-se igual a zero o tempo todo. Para isso acontecer, o helicóptero deveria girar no sentido contrário ao sentido da hélice. Isto não acontece porque em sua cauda é colocada outra hélice na posição vertical em relação ao solo. Quando esta é coloca em movimento, sua conservação de momento angular faz com que o helicóptero tente girar novamente no sentido contrário, anulando o primeiro movimento e ficando então estabilizado.
Note que em acidentes em que a aeronave perde esta hélice traseira, ela cai realizando um movimento de rotação.
Este conhecimento é também aplicado em equipamentos chamados Giroscópios (Figura 7), utilizados para orientação de navios e aeronaves.

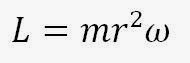


Nenhum comentário:
Postar um comentário
Dê sua opinião!